Prolactin and Progesterone
Probabalistic Decision making
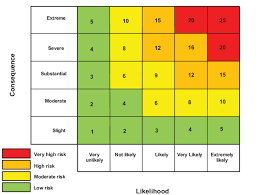
Probabilistic decision making under uncertainty is a crucial aspect of various fields including finance, medicine, engineering, and even our daily lives. In essence, it is the process of making informed decisions based on uncertain and probabilistic information. This approach integrates statistical analysis, probability theory, and risk assessment to evaluate different outcomes and make optimal choices.
One of the primary advantages of probabilistic decision making is that it helps to quantify the uncertainty inherent in any decision-making process. By assigning probabilities to different possible outcomes, decision-makers can gain a clearer understanding of the risks and rewards associated with each option.
For instance, in the field of finance, investors use probabilistic models to assess the likelihood of different investment outcomes. By evaluating the probability distribution of returns, they can make more informed decisions about where to allocate their resources. Similarly, in the field of medicine, doctors use probabilistic models to assess the likelihood of various diagnoses and treatment outcomes. This enables them to make better decisions about patient care.
There are several methods and tools available for probabilistic decision making under uncertainty. One common approach is the use of decision trees, which visually represent different decision options and their associated probabilities and outcomes. Another widely used method is the Monte Carlo simulation, which uses random sampling to generate a range of possible outcomes based on the input probabilities.
Despite its advantages, probabilistic decision making under uncertainty is not without its challenges. One of the main difficulties is that it requires accurate and reliable data to generate the probability distributions for different outcomes. In many cases, such data may be scarce or unreliable, making it difficult to generate accurate probability estimates. Additionally, the complexity of the probabilistic models can sometimes make it difficult for decision-makers to interpret the results and make informed choices.
In conclusion, probabilistic decision making under uncertainty is an essential tool for evaluating the risks and rewards associated with different options and making informed choices. By integrating statistical analysis, probability theory, and risk assessment, this approach helps to quantify the uncertainty inherent in any decision-making process and enables decision-makers to make more informed and rational choices. However, it is important to be aware of the challenges associated with this approach, including the need for accurate and reliable data and the potential complexity of the probabilistic models.
Let’s take an example from the business world to illustrate probabilistic decision-making. Imagine a company considering the decision to launch a new product. There are two options: launch the product or don’t launch the product. The outcome depends on the market’s response, which could be positive or negative.
Here’s a table representing the decision matrix:
| Decision | Market Response | Probability | Payoff | Expected Value |
| Launch | Positive | 0.6 | $1,000,000 | $600,000 |
| Launch | Negative | 0.4 | -$500,000 | -$200,000 |
| Don’t Launch | Positive | 0.6 | $0 | $0 |
| Don’t Launch | Negative | 0.4 | $0 | $0 |
In this example, the Expected Value (EV) is calculated by multiplying the probability of the outcome by the payoff for each decision-outcome pair. The decision with the highest expected value is usually the preferred choice.
From the table, we can see that launching the product has an expected value of $400,000 ($600,000 - $200,000), while not launching the product has an expected value of $0. Therefore, based on this analysis, the company should decide to launch the new product.
This example illustrates how probabilistic decision-making can be used to quantify the risks and rewards associated with different options and make more informed choices.












Leave a comment